期望效用函数理论

期望效用函数理论是20世纪50年代,冯·纽曼和摩根斯坦(Von Neumann and Morgenstern)在公理化假设的基础上，运用逻辑和数学工具，建立了不确定条件下对理性人(rational actor)选择进行分析的框架。

理论分析

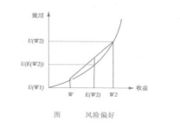
考虑两人的博弈(两人零和博弈)，二者出同样多的钱(100元)赌博，赢者变成200元，输者为0。不考虑其他因素情况下，输赢概率均为0.5，期望效用E(u)=0.5×200+0.5×0=100。双方的效用 $0.5 imes u_1+0.5 imes u_2=0.5(u_1+u_2)$ ，u1,u2为两种状态下的边际效用(如上图)。比赌博前的u1少了 $riangle u_1=0.5(u_1-u_2)$ 。如果一个人拥有200元，再拿出100元进行赌博，其损失效用为 $riangle u_2=0.5(u_2-u_3)$ ，比较 $riangle u_1, riangle u_2$ 如下：

$riangle u_1=0.5(u_1-u_2)=0.5(int_{200}^{100}u(x)dx-int_{300}^{200}u(x)dx)$

对

$int_{300}^{200}u(x)dx$

作变量替换t=x-100，得

$int_{300}^{200}u(x)dx=int_{200}^{100}u(t+100)dt=int_{200}^{100}u(x+100)dx$

$riangle u_1=0.5int_{200}^{100}[u(x)-u(x+100)]dx=0.5int_{200}^{100}-u^{prime}(mu_1)100dx=-0.5u^{prime}(mu_1)100^2,muin(100,300)$

$riangle u_2=0.5(int_{300}^{200}u(x)dx-int_{400}^{300}u(x)dx)=0.5int_{200}^{100}u(x+100)dx-int_{200}^{100}u(x+200)dx=0.5int_{200}^{100}u[(x+100)-u(x+200)]dx=-0.5u^{prime}(mu_2)100^2,$

$mu_2in(200,400)$

且100 < μ1 < μ2 < 400,

$riangle u_2- riangle u_1=[u^{prime}(mu_1)-u^{prime}(mu_2)]100^2=frac{1}{2}u^{primeprime}(mu)100^2,100^2<mu<400.$

当u为凹函数时 $u^{primeprime}(mu) />0$ ，当u是凸函数时 $u^{primeprime}(mu)<0$ ，当u是直线时， $u^{primeprime}(mu)=0$ 。所以当 $riangle u_2- riangle u_1 />0$ 时，u为凸函数; $riangle u_2- riangle u_1<0$ 时，u为凹函数; $riangle u_2- riangle u_1=0$ 时，u为直线。

由此可见， $riangle u_2- riangle u_1<0$ 时，即一个富人拿出一部分钱去赌博所损失的效用要低于一个穷人拿出同样的钱去赌博所损失的效用。也就是说富人更经得起这种赌博带来的效用损失。因而u是凹函数。

主要挑战

EU理论及SEU理论描述了“理性人”在风险条件下的决策行为。但实际上人并不是纯粹的理性人，决策还受到人的复杂的心理机制的影响。因此，EU理论对人的风险决策的描述性效度一直受到怀疑。例如，EU理论难以解释阿莱悖论、Ellsberg悖论等现象;没有考虑现实生活中个体效用的模糊性、主观概率的模糊性;不能解释偏好的不一致性、非传递性、不可代换性、“偏好反转现象”、观察到的保险和赌博行为;现实生活中也有对EU理论中理性选择上的优势原则和无差异原则的违背;实际生活中的决策者对效用函数的估计也违背EU理论的效用函数。

另外，随着实验心理学的发展，预期效用理论在实验经济学的一系列选择实验中受到了一些“悖论”的挑战。实验经济学在风险决策领域所进行的实验研究最广泛采取的是彩票选择实验(lottery-choice experiments)，即实验者根据一定的实验目标，在一些配对的组合中进行选择，这些配对的选择通常在收益值及赢得收益值的概率方面存在关联。通过实验经济学的论证，同结果效应、同比率效应、反射效应、概率性保险、孤立效应、偏好反转等“悖论”的提出对预期效用理论形成了重大冲击。

理论扩展

研究者针对以上问题提出了以下几种使EU理论一般化的方式:

(1)Karmark(1978)提出主观权重效用(Subjectively Weighted Utility，SWU)的概念，用决策权重替代线性概率，这可以解释Allais问题和共同比率效应，但不能解释优势原则的违背;

(2)扩展性效用模型(generalized utility model)。该类模型的特点是针对同结果效应和同比率效应等，放松预期效用函数的线性特征，或对公理化假设进行重新表述，模型将用概率三角形表示的预期效用函数线性特征的无差异曲线，扩展成体现局部线性近似的扇行展开。这些模型没有给出度量效用的原则，但给出了效用函数的许多限定条件。

(3)Kahneman和

1.风险偏好

风险偏好表明

CE 被称作确定性等值(Certainty. Equivalent)，即消费者为达到期望的效用水平所要求保证的财产水平。若某人的财富效用函数为u(x)，而一个赌局对某人的效用为E(u(x))，则有一个CE值能够满足：u(CE)=E(u(x))。称CE为某人在该赌局中的确定性等值。

风险问题的解决——

案例一:期望效用函数理论在就业管理中的应用

一、就业期望效用函数的构造

从不确定性出发，考虑人们的偏好与效用函数就得引进概率P。概率的效用函数表达式叫期望效用函数，如果把期望效用函数与大学生择业、就业结合就可以较简单地构造出就业期望效用函数探讨大学生就业的现象机制一般来讲是在条件确定时进行的经验或者理性的推导。但是，许多场合，那种以完全确定为前提的分析是不现实的。事实上，我们知道，毕业生在决策时，对于选择的后果是不完全知道的，具有不确定性，要冒一定的风险。

毕业生的决策是取决于他(她)关于选择某一个工作岗位的概率分布的主观猜测。如果他主观认为选择某一工作发展前景概率更高，那么，它就会选择，否则另谋出路。这就是我们必须从不确定性出发，考虑消费者的偏好与效用函数就得引进概率P使之变成期望效用函数。如果你选择的工作对象是两家IT公司，收入见下表。

	结果1		结果2
	可能性(P)	收入	可能性(P)	收入
工作A:(佣金制)	0.6	2000	0.4	1000
工作B:(固定资金)	0.95	1500	0.05	500

期望收入=(结果1的概率)×(结果1的收入)+(结果2的概率)×(结果2的收入)。工作A=1600。工作B=1450则你应该选择工作A，而期望效用(expected utility)一般在单赌的情况下值为u(g)=pu(A)+(1-P)u(B)当u(g1) > u(g2)时，则可认为毕业时在g_1与g_2之间更偏好g_1。也就是说，当寻找工作的毕业生有多种未知的情况，而要选择时，他们能够依靠期望效用的极大化来代表分析自己的主观选择。如果选择工作的结果有，n个可能性，即 $A=(a_1,a_2,ldots,a_n)$ ，同时对u(ai)(i=1,2,……,n)赋值，代人构造的就业期望效用函数。如果 $a_ />a_2>ldotsldots>n$ 即对毕业生来说，ai最好，an最次。如果学生把ai看成是a1与an的一个线性组合一样好，在他看来，任一个可能结果ai(i=1,2,……,n)总不外是与最好的结果与最次的结果之间的某种组合一样好，即ai～ $(P_icdot a_1,(1-P_i)a_n)$ 。

令u(ai) − = pi即用毕业生心里那个使a与某个单赌等价的最好事件发生概率P_i来定义u(a_i)则可构建就是期望效用函数为： $u(s)=sum_{i=1}^nP_iu(a_i)$ 就业期望效用函数的意义在于，当大学生面临不确定性的择业、就业选择时，他可以依靠期望效用的极大化来分析自己的选择是否合理可行，至少可以对目前的状况做较规范的分析。

二、效用函数应用实例

假设目前市场上由三份工作可以选择，它们的工资分别为A=(3000元，1500元，1000元)括号中的a1 = 3000,a2 = 1500,a3 = 1000，分别表示可能发生的三种结果，这里a1最好，a3最次。

如果问自己：当a发生的概率(p)等于多少时使你认为a(i=1，2，3)与(p,a1,a2)元差异?如果回答是：3000元～(1×(3000元)，0×(1000元)，1500元～(0.6×(3000元)，0.4×(1000元))，1000元～(0×(3000元)，1×(1000元))那么可以定义：

u=(3000元) = u(a1) = 1

u=(1500元) = u(a2) = O.6

u=(1000元)=u = (a3) = O

现在可以比较不同寻职格局了。比如：

$S_1=(0.2 imes1500,0.8 imes3000)$
$S_2=(0.07 imes1000,0.03 imes1500,0.9 imes3000)$

则u(S1) = 0.2u(1500) + 0.8u(3000) = 0.92

$u(S_2)=0.07u(1000)+0.03u(1500)+0.9 imes u(3000)=0.918$

由于u(S1) > u(S2)即S1的期望效用大于S2的期望效用，所以你=定会偏好于选择S1。因此就业者可以通过自己对某=行业的了解及心理自测的评价，利用就业期望效益较合理评估自己的想法，寻找更多的机会和更合适的工作岗位。

故事内容仅供参考，如果您需要解决具体问题
（尤其在法律、医学等领域），建议您咨询相关领域专业人士。

如果您认为本故事还有待完善，请编辑

上一篇贺州市文学艺术界联合会下一篇平南铁路

期望效用函数理论

目录

理论分析

主要挑战

理论扩展

附件列表

标签

同义词